Did you know that the more ice cream that is consumed in the world, there are more deaths from drowning? These relationships, between ice cream and drowning deaths, are examples of correlation. A deeper question is if one event causes the other event. The concept of correlation will be discussed in this chapter. How we distinguish how strong a correlation is between two quantities is important and can lead to actually predicting future events with surprising accuracy. We will measure the strength of correlation with what is called Pearson’s correlation coefficient. We will utilize the graphing calculator to obtain this value. Pearson’s correlation coefficient is a value 𝑟 such that $−1\leq r \leq 1$. The closer $r$ is to positive $1$, we say there is a strong positive correlation. The closer $r$ is to negative $1$, we say there is a strong negative correlation. The closer $r$ is to $0$, we say there is no correlation. If $r$ is close to positive $1$ or close to negative $1$, we can more confidently predict future events. Examples of each are shown below.

Positive Correlation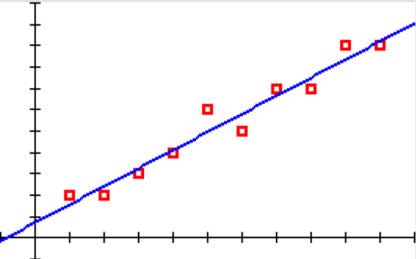

No Correlation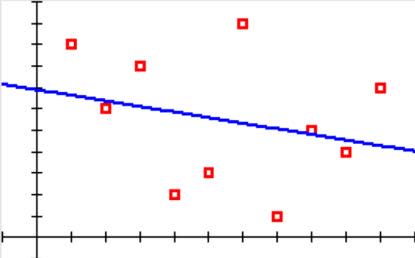

Negative Correlation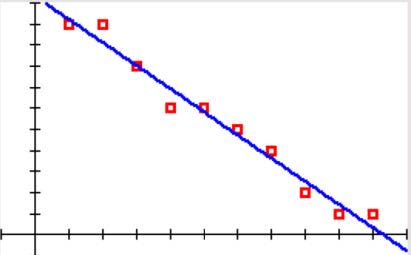

The more closely the linear regression line “hugs” the data values, the stronger the correlation is, either positive or negative.

The linear regression line is the line that most closely resembles a trend in the data. The equation of this line can be calculated analytically but for purposes of this course, technology will be used to obtain it. 

Example 1: The amount of time $x$, in minutes, it takes a student to correctly answer $y$ questions on five exams is given as: $(1,4 ),(2,6),(3,5),(4,7),(6,8)$. Determine how many questions, approximately, the same student will answer correctly after $8$ minutes?

Explanation: We need to find the linear regression line. This is done by plotting these points in the stat-Edit option on the calculator. Calculating the regression line can be done using stat-Calc-LinReg $(ax+b)$.

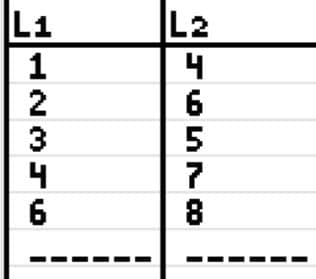
The line of best fit is given by $y=0.743x+3.62$. Thus after $8$ minutes, we could expect a student to answer $y=0.743(8)+3.62=9.56$ questions correctly, in other words, $9$ or $10$ questions correctly. Since $r=0.904$, we feel confident in our prediction.