Circular motion

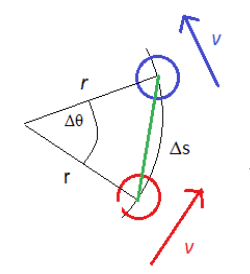
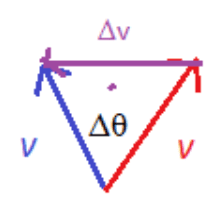
When a force is at right angles to a body’s velocity circular motion can occur.

Circular motion at constant speed: period, frequency, angular displacement and angular velocity.

• The velocity has the same magnitude but changes direction. In time $\Delta t$ the body moves, and the radius moves through an angle $\Delta \theta$.
• The angular velocity $(\omega)$ is the angle swept out by per unit time. The unit of angular velocity is the radian $s^{−1}$.
  $\omega = \Delta \theta/\Delta t$
• The time period $\rm (T)$ is the time taken to complete one circle. The unit of the time period is the second:
  $\omega = 2\pi/\rm T$
• The frequency is the number of complete revolutions per unit time (e.g. the second).
  • $f = 1/\mathrm T$
  • $\omega = 2\pi f$
• In a time, $\rm T$, the body completes one full cycle.
  • $\text{distance} = 2\pi r$
  • $v = 2\pi r/\rm T$ and $v = \omega r$

• Consider the similar triangles:

If $\Delta \theta$ and $\Delta t$ are small $r \Delta \theta=\Delta s=v \Delta t$ $\Delta \theta=v \Delta t / r$
$\Delta \theta=v \Delta t / r=\Delta v / v$
$\qquad\Delta v / \Delta t=v^{2} / r$

If $\Delta \theta$ and $\Delta v$ are small $v\Delta\theta =   \Delta v$
$\Delta\theta = \Delta v/ v$
$\Delta\theta = v\Delta t /r  = Δv/v$
$\qquad\Delta v /\Delta t = v^2/r$

The centripetal acceleration
$a = \Delta v / \Delta t =v^{2} =\omega^{2} r$

The centripetal acceleration has the same direction as $\Delta v$: toward the centre of the circle.

• The net force has the same direction as the centripetal acceleration and is directed towards the centre of the circle. The centripetal force $= ma = mv^2/r= m\omega^2r$

$\rm T_{1}+m g=m v^{2} / r$
$\rm T_{1}=m v^{2} / r-m g$

As the mass approaches the top kinetic energy $\rm \left(E_{K E}\right)$ is converted into potential energy $\rm \left(E_{P E}\right)$, leading to a reduction in speed.
The minimum speed necessary for a complete circle is when the weight of the ball is enough to provide the centripetal force when $\rm T_{1}=0$ $\rm m g=m v^{2} / r$
$\rm g =v^{2} / r$
$\rm T_{2}-m g=m v^{2} / r$
$\rm T_{2}=m v^{2} / r+m g$