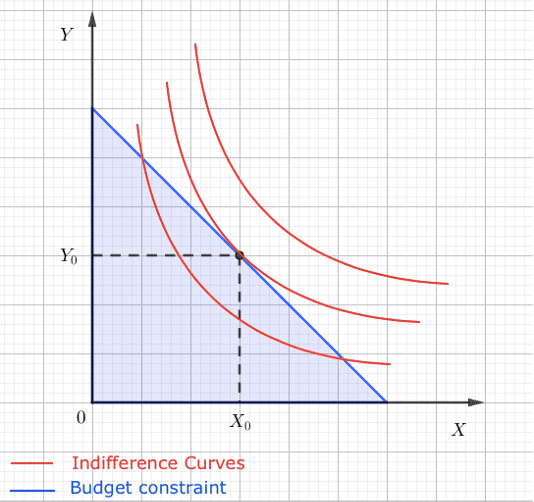
Consumer decisions

The utility function measures the satisfaction of the consumer obtains from the consumption of a good or a service. This function is used in microeconomics to analyze human behavior.

The consumer’s goal is to maximize his utility subject to the constraint of household incomes and product prices.

Assumptions:

  • Budget constraint and product prices
  • Rational behavior
  • Preferences are known and measurable

Problem:

$\mathrm{Max~ U}=f\rm (X, Y)$
s.t. $\rm P_{X} \times X+P_{Y} \times Y \leq I$
where:
$\rm P_{X}$ is the price of good $\rm X$,
$\rm P_{Y}$ is the price of good $\rm Y$,
$\rm X$ is the quantity of good $\rm X$,
$\rm Y$ is the quantity of good $\rm Y$,
$\rm I$ is the household income.

Solving the problem: 

  • Create a new equation with the information given (using the Lagrange Multiplier method): $$L(X, Y, \lambda)=f(X, Y)-\lambda\left(I-P_{X} \times X-P_{Y} \times Y\right)$$
  • The first-order condition (to find the extremum): 

$\left\{\begin{array}{l}\rm \frac{\partial L(X, Y)}{\partial X}=0 \\ \rm \frac{\partial L(X, Y)}{\partial Y}=0 \\ \rm \frac{\partial L(X, Y)}{\partial \lambda}=0\end{array} \Leftrightarrow\left\{\begin{array}{c}\rm \frac{\partial f(X, Y)}{\partial X}-\lambda P_{X}=0 \\ \rm \frac{\partial f(X, Y)}{\partial Y}-\lambda P_{Y}=0 \\ \rm I-P_{X} \times X-P_{Y} \times Y=0\end{array}\right.\right.$

  • The maximum is the solution of the system above (it is assumed that the solution is a maximum).

Producer decisions

The producer’s goal is to maximize his profit subject to cost constraint.

Problem:

$\operatorname{Max} \pi=\pi(x)=\mathrm R(x)-\mathrm C(x)$
where:
$\pi(x)$ is the profit,
$\mathrm R(x)$ is the firm's revenue
$\mathrm R(x)=\mathrm P \times x$ where $\rm P$ is the product price and $x$ the number of units of product sold,
$\mathrm C(x)$ is the firm's cost
$\mathrm C(x)=\mathrm{V C}(x)-\rm F$ where $\mathrm{V C}(x)$ is the variable cost and $\rm F$ the fixed cost
Solving the problem:

The first-order condition (to find the extremum): $\pi^{\prime}(x)=0$
$\pi^{\prime}(x)=\mathrm R^{\prime}(x)-\mathrm C^{\prime}(x)=\mathrm{M R}(x)-\mathrm{M C}(x)$ where $\rm M$ stands for "marginal"
$\mathrm{M R}(x)=$ marginal revenue
$\mathrm{M C}(x)=$ marginal cost
$\pi^{\prime}(x)=0 \Leftrightarrow \mathrm R^{\prime}(x)-\mathrm C^{\prime}(x)=0$
$\mathrm{M R}(x)=\mathrm R^{\prime}(x)=\mathrm P$
$\mathrm{M C}(x)=\mathrm C^{\prime}(x)=\mathrm{V C}^{\prime}(x)-\mathrm F^{\prime}=\mathrm{V C}^{\prime}(x)$ because $\rm F$ is the fixed cost (constant), so $\rm F^{\prime}=0$.
Thus, the first-order condition is equivalent to write: $\mathrm{P=V C}^{\prime}(x)$

The second-order condition (to prove that it is a maximum): $\pi^{\prime \prime}(x)<0$ to find a maximum $\pi^{\prime \prime}(x)<0 \Leftrightarrow \mathrm R^{\prime \prime}(x)-\mathrm C^{\prime \prime}(x)<0$ $\Leftrightarrow$ $0-\mathrm C^{\prime \prime}(x)<0$ $\Leftrightarrow$ $-\mathrm C^{\prime \prime}(x)<0$ $\Leftrightarrow$  $\mathrm C^{\prime \prime}(x)>0$