In this unit it is assumed that students understand that $360°$ around a circle is equivalent to $2\pi$ radians. Recall the area of a circle with radius $r$ is given by $\mathrm A =\pi r^2$. Suppose we do not want to know the area of the entire circle, but just a piece of the circle, or “sector” of the circle as shown below:

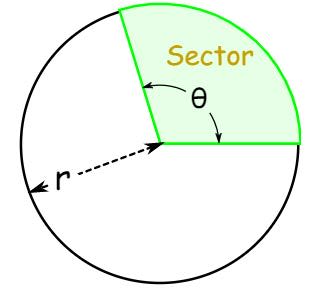
In this case, the central angle $\theta$ is not $2\pi$ radians but a proportion of $2\pi$ radians. The exact proportion is $\dfrac{\theta}{2\pi}$. Thus the area of the sector is the proportion of the area of the circle. In other words, the area of a sector is given by: $\mathrm A=\pi r^2\cdot \dfrac{\theta}{2\pi} =\dfrac{1}{2}r^2\theta$ where $r$ is the radius of the circle and $\theta$ is the central angle in radians.

Likewise, recall the circumference of a circle with radius $r$ is given by $\mathrm A=2\pi r$. Suppose we do not want to know the circumference of the entire circle, but just a piece of the circle, or “arc $\rm L$” of the circle as shown below:

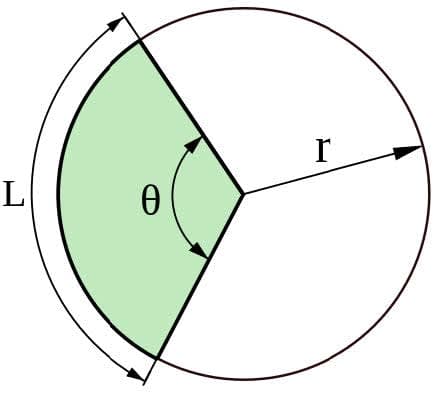
In this case, the central angle $\theta$ is not $2\pi$ radians but a proportion of $2\pi$ radians. The exact proportion is $\dfrac{\theta}{2\pi}$. Thus the length of arc $\rm L$, is a proportion of the circumference of the circle. In other words, the length of the arc is given by: $\mathrm L = 2\pi r \cdot \dfrac{\theta}{2\pi} = r \theta$ where $r$ is the radius of the circle and $\theta$ is the central angle in radians.

Example 1: Determine the area of the shaded region (sector) in the diagram below.

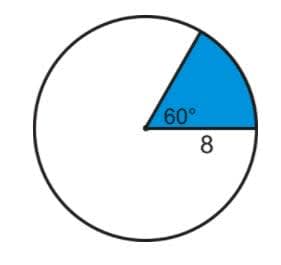
Explanation: We must first convert $60°$ into radians. $60°=60\cdot \dfrac{\pi}{180}=\dfrac{\pi}{3}$ radians. Since the radius is $8$, we can use the formula for the area of a sector:

$\mathrm A=\dfrac{1}{2}(8)^2\dfrac{\pi}{3}$
$\mathrm A = \dfrac{1}{2}\cdot 64\cdot \dfrac{\pi}{3}$
$\mathrm A=\dfrac{64\pi}{6}$
$\mathrm A=\dfrac{32\pi}{3}$ units squared.

Example 2: A circular garden is to be constructed in a city center. Pedestrians can walk along a certain portion of the garden for observations and pictures. If the pedestrian walkway along the edge of the circle measures $24\pi$ meters and the central angle of the garden extending to both endpoints of the walkway is $45°$, determine the radius of the garden.

Explanation: $45°=45\cdot \dfrac{\pi}{180} = \dfrac{\pi}{4}$ radians. Thus, $24\pi = r\cdot \dfrac{\pi}{4}$ $\Rightarrow$ $96\pi = r\pi$ $\Rightarrow$ $r=96$ meters.