Oscillations électriques forcées

I. Courant alternatif sinusoïdal

Définition

On appelle courant alternatif sinusoïdal un courant dont l'intensité est une fonction sinusoïdale du temps : $i = I_{\rm m} \sin(\omega t + \varphi)$ ou $i = I_{\rm m} \cos(\omega t + \varphi)$ avec

$I_{\rm m}$ est l'intensité maximale en $\rm A$
$\omega$ est la pulsation en rad. ${\rm s}^{-1}$
$\varphi$ est la phase à l'origine des dates $t = 0$
$\omega t + \varphi$ est la hase à la date $t$

Intensité et tension instantanées

Elles sont de la forme :

$i = I_{\rm m} \sin(\omega t + \varphi)$ et $u = U_{\rm m} \sin(\omega t)$

$i = I_{\rm m} \sin(\omega t )$ et $u = U_{\rm m} \sin(\omega t + \varphi)$ avec $\varphi_{u/i}$= $\varphi$.

$\varphi$ est la phase de $u$ par rapport à $i$

Si $\varphi > 0$ $u$ est en avance par rapport à $i$
Si $\varphi < 0$ $u$ est en retard par rapport à $i$
Si $\varphi = 0$ $u$ et $i$ sont en phase

Intensité et tension instantanées

L'intensité efficace $I$ est liée à l'intensité maximale $I_{\rm m}$ par $I = \dfrac{I_{\rm m}}{\sqrt{2}}$
La tension efficace $I$ est liée à la tension maximale $U_{\rm m}$ par $U = \dfrac{U_{\rm m}}{\sqrt{2}}$

NB : Les valeurs efficaces sont déterminées à partir de l'ampèremètre et du voltmètre utilisés en mode alternatif.

Les valeurs maximales déterminées à partir des oscillogrammes

Impédance d'un circuit

En régime sinusoïdal, On appelle impédance $Z$ d'un circuit le rapport $Z = \dfrac{U_{\rm m}}{I_{\rm m}} = \dfrac{U}{I}$ avec $Z$ en ohm

II. Étude d'un circuit (R, L, C) série

Équation différentielle

Supposons $u = U_{\rm m} \cos(\omega t + \varphi)$et $i = I_{\rm m} \cos(\omega t)$

Loi des tensions :

$u = U_{\rm R} + U_{\rm L} + u_{\rm c} \Rightarrow u = \rm R i + L \dfrac{di}{dt} + \dfrac{q}{C} \Rightarrow u = \rm R i + L \dfrac{di}{dt} + \dfrac{1}{C} \displaystyle \int i dt$ Car $i = \dfrac{dq}{dt} \Rightarrow q = \displaystyle \int i dt$

$U_{\rm m} \cos(\omega t + \varphi) = \rm R I_{\rm m} \cos(\omega t) + L \omega I_{\rm m} \cos(\omega t + \dfrac{\pi}{2}) + \dfrac{I_{\rm m}}{\omega C} \cos(\omega t - \dfrac{\pi}{2})$

Caractéristiques du circuit (R, L, C)

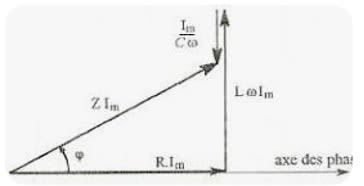
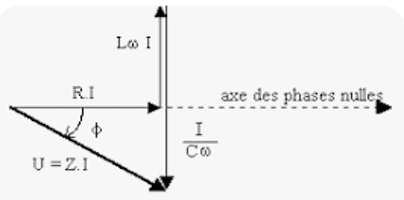
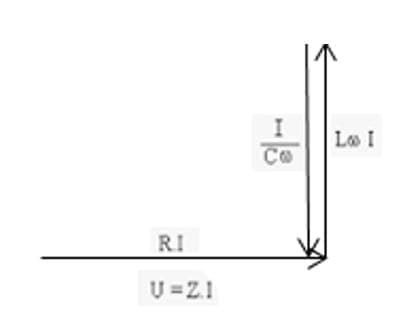
Construction de Fresnel

L'origine des phases étant l'axe de l'intensité. Trois cas peuvent se présenter :

1^er cas : $L\omega > \dfrac{1}{C\omega}$ : circuit inductif

2^e cas : $L\omega < \dfrac{1}{C\omega}$ : circuit capacitif

3^e cas : $L\omega = \dfrac{1}{C\omega}$ : circuit résistif (circuit en résonance)

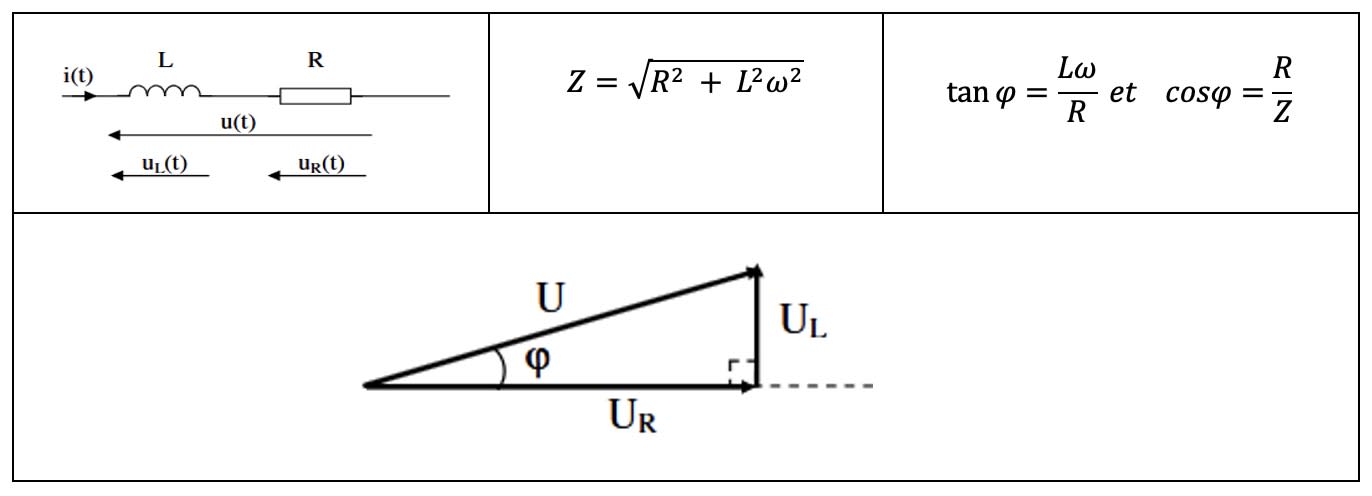
Impédance du dipôle (R, L)

Considérons le 1^er cas

D'après Pythagore, $U_{\rm m}^2 = (\rm R I_{\rm m})^2 + (L\omega - \dfrac{1}{C\omega})^2 I_{\rm m}^2 \Rightarrow U_{\rm m}^2 = (\rm R I_{\rm m})^2 + (L\omega - \dfrac{1}{C\omega})^2 I_{\rm m}^2$

$U_{\rm m}^2 = \rm R^2 I_{\rm m}^2 + (L\omega - \dfrac{1}{C\omega})^2 I_{\rm m}^2 = Z^2 I_{\rm m}^2 \Rightarrow Z = \sqrt{\rm R^2 + (L\omega - \dfrac{1}{C\omega})^2}$

Déphasage de la tension $u$ par rapport à l'intensité $i$

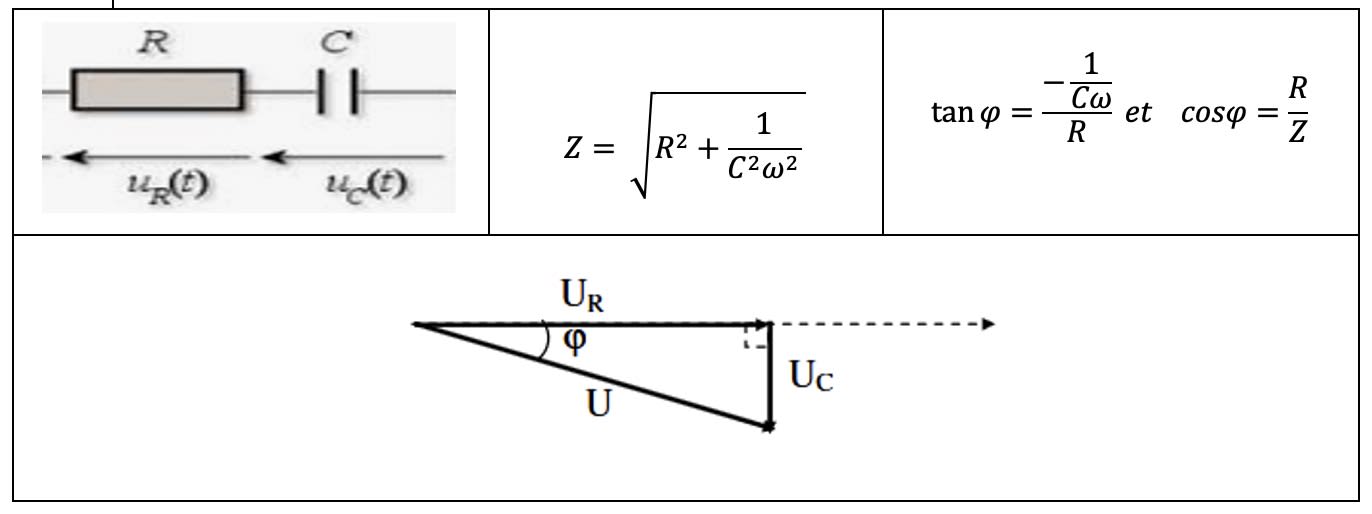
$\tan \varphi = \dfrac{L\omega - \dfrac{1}{C\omega}}{\rm R}$ et $\cos \varphi = \dfrac{\rm R}{Z}$

NB : Si la résistance $r$ de la bobine n'est pas négligeable, on remplace la résistance $\rm R$ par la résistance totale $\rm R + r$ du circuit dans l'expression de l'impédance et du déphasage

$\tan \varphi = \dfrac{L\omega - \dfrac{1}{C\omega}}{\rm R + r}$ et $\cos \varphi = \dfrac{\rm R + r}{Z}$

Étude de cas particuliers

Circuit (R, L)

Circuit (R, C)

III. Résonance électrique

Condition de résonance

Pour un circuit (R, L, C), la résonance se produit lorsque la pulsation imposée par le générateur est égale à la pulsation propre $\omega_{\rm o}$ du circuit.

Grandeurs caractéristiques de la résonance

Pulsation propre

À la résonance, l'impédance $Z$ est minimale. $L\omega = \dfrac{1}{C\omega} \Rightarrow LC\omega^2 = 1 \Rightarrow \omega^2 = \dfrac{1}{LC} \Rightarrow \omega = \dfrac{1}{\sqrt{LC}}$

$\omega = \omega_{\rm o}$

Période propre

$T_{\rm 0} = \dfrac{2\pi}{\omega_{\rm 0}} \Rightarrow T_{\rm 0} = 2 \pi \sqrt{LC}$

Fréquence propre

$N_{\rm 0} = \dfrac{1}{T_{\rm 0}} \Rightarrow N_{\rm 0} = \dfrac{1}{2 \pi \sqrt{LC}}$

Intensité efficace

$I_{\rm 0} = \dfrac{U}{\rm R}$ car à la résonance $Z = \rm R$

Déphasage

$\varphi = 0 \Rightarrow u$ et $i$ sont en phase

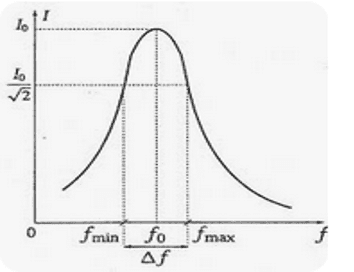
Courbe de résonance

C'est la courbe de l'intensité efficace $I$ en fonction de la pulsation $\omega$ ou de la fréquence $f$

$I = f(\omega)$ou $I = g(f)$

Bande passante

C'est le domaine des pulsations pour lesquelles $I \geq \dfrac{I_{\rm 0}}{\sqrt{2}}$. La largeur de la bande passante est la différence entre les pulsations $\omega_1$ et $\omega_2$ ou les fréquences $f_1$ et $f_2$ pour lesquelles $I = \dfrac{I_{\rm 0}}{\sqrt{2}}$

$\Delta \omega = \omega_2 - \omega_1 = \dfrac{\rm R}{L}$ ; $\Delta f = f_2 - f_1 = \dfrac{\rm R}{2 \pi L}$

Facteur de qualité

On appelle facteur de qualité ou coefficient de surtension le rapport :

$Q = \dfrac{\omega_{\rm o}}{\Delta \omega} \Rightarrow Q = \dfrac{L\omega_{\rm o}}{\rm R} ; Q = \dfrac{f_{\rm o}}{\Delta f} \Rightarrow Q = \dfrac{1}{\rm R} \sqrt{\dfrac{L}{C}}$

Aux bornes de la bobine : $Q = \dfrac{U_{\rm L}}{U}$

Aux bornes du condensateur $U_{\rm c}$ est telle que $Q = \dfrac{U_{\rm c}}{U}$

Un circuit est d'autant plus sélectif que le facteur de qualité $Q$ est grand. Mais si $Q$ est trop grand, il y a risque de surtension aux bornes du condensateur ou de la bobine

Puissance consommée et facteur de puissance

La puissance consommée par le dipôle en régime sinusoïdal est $P_{\rm m} = U I \cos \varphi$

Cette puissance est le produit de deux facteurs

$P_{\rm a} = U I$ est la puissance apparente exprimée en Volt. Ampère (V. A)
$\cos \varphi$ est le facteur de puissance du circuit

Étude des cas particuliers

Dipôle	$\varphi$	$\cos \varphi$	$P_{\rm m}$
Résistance $\rm R$	$0$	$1$	$UI = \rm R I^2$
Bobine pure	$\dfrac{\pi}{2}$	$0$	$0$
Condensateur parfait	$\dfrac{\pi}{2}$	$0$	$0$
Circuit (R, L, C) série	$\cos^{-1} \dfrac{\rm R}{Z}$	$\dfrac{\rm R}{Z}$	$\rm R I^2$

Une bobine pure et un condensateur parfait ne consomment pas d'énergie

Dans un circuit (R, L, C) série toute la puissance moyenne est consommée dans la résistance par effet Joule.